REPRESENTATION DES CONNAISSANCES
Introduction
Dans le chapitre précédant nous avons vu que la mise en place d'un système productique réellement intégré suppose la définition d'un modèle complet de la filière technologique visée. Or, qui dit modèle, dit représentation de ce modèle. Les données et processus utilisés en ingénierie étant de natures très diverses et complexes, il nous faut trouver un modèle assez riche pour pouvoir les représenter de façon complète. Nous aborderons donc ici plus particulièrement le problème de la représentation des connaissances.
Le domaine de la représentation des connaissances étant l'un des axes de recherche central en intelligence artificielle, nous verrons donc ce que l'intelligence artificielle peut nous apporter pour modéliser les connaissances en ingénierie. Nous nous placerons plus particulièrement dans le cadre de l'approche dite objets qui nous semble la plus riche et la mieux appropriées.
Après avoir présenté les concepts clefs de cette approche, et avoir établi une typologie des langages orientés objets, nous aborderons plus particulièrement le problème de la représentation des connaissances en ingénierie.
Nous passerons alors en revue les caractéristiques principales des objets et données manipulés en ingénierie. Nous montrerons alors qu'il est nécessaire d'aller plus loin qu'une simple représentation de type attribut/valeur et que la représentation d'objets industriels nécessitent la représentation d'informations sur les données, c'est à dire la représentation de méta connaissances.
Nous terminerons en présentant les différents modèles et mécanismes permettant de représenter ces méta-informations au niveau des objets. Parmi ces modèles, nous présenterons plus en détail le modèle PDM. En effet ce modèle offre un bon compromis entre efficacité du langage et son expressivité, et il est à la base du modèle objet utilisé dans l'un des système de gestion de base de données que nous avons utilisé : G-Base.
Représentation des connaissances
La représentation des connaissances est au cur des recherches en psychologie cognitive et en intelligence artificielle. Sa problématique peut s'exprimer ainsi [Ferber 89].
· Quelles sont les catégories conceptuelles a priori de la pensée et du raisonnement ?
· Quels sont, à partir de ces catégories fondamentales, les mécanismes pratiques qu'un système (individu ou machine) emploie de façon à pouvoir résoudre des problèmes, prendre des décisions et parvenir à ses fins ?
Ces deux interrogations se retrouvent dans tous les problèmes d'intelligence artificielle. Leur résolution nécessite de faire un certain nombre de choix.
1) Point de vue théorique : choix d'un formalisme permettant de représenter et de raisonner sur les connaissances.
2) Point de vue cognitif : choix des concepts nécessaires à la description et à la résolution du problème étudié.
3) Point de vue Implémentation : choix de moyens pratiques permettant la représentation efficace des données par un programme.
4) Point de vue méthodologique : choix des moyens permettant l'acquisition et la validation des connaissances.
Nous aborderons le point (1) en évoquant les différents paradigmes de représentation utilisés en intelligence artificielle. Nous montrerons qu'une approche multi-paradigmes nous semble nécessaire, et que dans ce cadre, le concept d'objets peut jouer un rôle intégrateur. Dans le cadre de l'approche objet, nous étudierons ensuite les points (2) et (3) pour caractériser les principaux concepts utilisés en ingénierie, et la façon de les représenter. Le point (4) sera abordé ultérieurement dans l'annexe III consacrée aux méthodologies de conception objet, les méthodes permettant l'identification, la modélisation et la validation des connaissances.
Les paradigmes de représentation
En informatique, il n'y a pas de langage universel. Au contraire, bien que tous les langages informatiques aient la même puissance calculatoire assimilable aux possibilités d'une machine de Turing, on continue à en voir apparaître de nouveaux presque chaque jour. Depuis le début de l'informatique avec le modèle impératif et séquentiel imposé par l'architecture dite de Von Neuman des premiers processeurs, de nombreux autres paradigmes de calcul ont été introduits. Chacun de ces paradigmes a été défini historiquement pour répondre à de nouveaux besoins, pour représenter de nouveaux types de données, ou permettre de programmer de nouvelles architectures de processeurs.
Procédural
L'approche procédurale est la première et la plus connue des techniques de programmation utilisée pour implanter des algorithmes. Pour cela elle offre un certain nombre de structures de contrôle prédéfinies telle que la séquence, le test, la boucle.
Fonctionnel
Cette approche trouve ses fondements mathématiques dans la théorie du l-calcul, basé exclusivement sur la notion de fonction. Son représentant le plus connu est le langage LISP.
Logique
Cette approche est intéressante, car elle permet immédiatement de dériver de nouveaux faits à partir de données de base grâce au principe de déduction. Cette approche est notamment représentée par le langage PROLOG [Giannesini et all 85].
Réseaux sémantiques
Issus des travaux de psychologie cognitive, ils utilisent un formalisme de graphe dans lequel les nuds représentent les concepts, et les arcs étiquetés figurent les relations entre ces concepts. Ils ont donné naissance à de nombreux systèmes : NETL, KL-ONE, etc.
Objet
Cette approche permet de prendre en compte à la fois l'aspect statique d'une connaissance, en définissant la structure d'un objet (ses attributs et ses liens avec d'autres objets), et son aspect dynamique, en définissant un ensemble d'opérations (les méthodes) applicables à un objet.
Multiparadigme
Chacune de ces approches offre un mode de pensée cohérent et unique, et chacune possède une élégante simplicité. Elles permettent ainsi d'analyser clairement un problème et de le résoudre. Mais cette simplicité devient un inconvénient lorsque l'on cherche à analyser un problème complexe. Chacun de ces paradigmes devient alors trop étroit et trop focalisé pour pouvoir s'appliquer facilement à tous les aspects du système étudié.
La résolution de problèmes complexes doit faire l'objet de l'utilisation simultanée de plusieurs de ces paradigmes. Chaque paradigme permettant alors de prendre en compte les aspects du système pour lequel il est le mieux adapté [Zave 89]. Il ne faut pas chercher à adapter à tout prix le paradigme au problème, mais au contraire choisir le ou les approches les plus appropriées selon le système étudié.
Cette idée a débouché notamment sur la création d'environnements de développement intégrant en leur sein plusieurs de ces paradigmes de programmation. On peut citer notamment la plupart des grands générateurs de systèmes experts tels que ART, KEE, KnowlegeKraft, SMECI, ou le sytème de conception "intelligent" ICAD, qui tous, intègrent plus ou moins la programmation par règles, la programmation fonctionnelle et les objets.
Au sein de cette approche multiparadigmes, les objets peuvent souvent jouer un rôle intégrateur. En effet, grâce au mécanisme d'encapsulation, ils sont à même d'absorber les concepts des autres paradigmes.
Les objets : un concept fédérateur
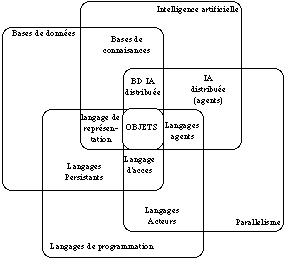
La notion d'objet s'impose de plus en plus comme une notion centrale en informatique, chaque domaine particulier mettant plus ou moins l'accent sur certaines particularités des objets, devenant un point de rencontre des différents domaines de l'informatique : les langages de programmation, les bases de données, l'Intelligence artificielle, et le calcul parallèle.
Les objets comme concept fédérateur.
Chacun de ces domaines a son propre point de vue, et utilise de façon différente les concepts liés à la notion d'objet, et aux points de rencontres de ces différentes technologies sont apparus de nouveaux concepts.
· La rencontre des bases de donnée et des langages de programmation a donné naissance aux langages objets persistants.
· La rencontre des langages de programmation et du calcul parallèle a donné naissance aux langages acteurs.
· La rencontre des techniques d'I.A. et du calcul parallèle a donné naissance à l'Intelligence Artificielle Distribuée (I.A.D.)
· La synthèse des techniques d'I.A et des bases de données est vite apparue nécessaire pour pouvoir stocker de grandes quantités de connaissances, et donc de constituer des bases de connaissances.
Les objets : pas une solution miracle
L'objet ne doit pas être considéré comme un nouveau paradigme de calcul. Il ne renouvelle pas les traitements et les algorithmes, mais ne les remet pas en cause non plus.
L'utilisation d'objets n'influe en rien dans la résolution de problèmes algorithmiques complexes : l'analyse numérique, l'optimisation, et plus généralement tous les problèmes mathématiques. Pour ce type de problèmes, l'utilisation d'un langage orienté objet ou celle d'un langage procédural de tel que FORTRAN, ne changera pas grand chose.
L'approche objet
Pour plus de détails, on trouvera une bonne introduction et un bon descriptif de l'état de l'art et des recherches dans ce domaine dans [Barthes et al.90].
"La notion d'objet, une fois exhibée, semble avoir toujours existé. La philosophie, à travers de nombreuses discussions sur sa nature, a toujours montré l'importance de l'être, notion essentielle pour la compréhension de la philosophie occidentale. A l'encontre de la logique mathématique moderne, la conception "objet" considère que la mise en relation est secondaire par rapport à la prééminence de la chose et de ses propriétés. Comme le signale Meinong [Meinong.60] dans sa théorie des objets, un objet ne peut être asserté ou postulé. Il n'est ni vrai ni faux. Il existe, tout du moins dans l'esprit des individus. Cela ne signifie pas qu'aucune relation, qu'aucune prédication n'est possible, bien au contraire, mais que celle ci est un objet comme un autre, et peut donc être décrite par ses propriétés." [Barthes et al.90]
Principe de l'approche objet
L'approche objet de la représentation des connaissances est fondée sur 3 propositions de bases, et un concept : celui de la réification.
Proposition 1 : un objet conceptuel est décrit par l'ensemble des attributs qui le caractérisent et des opérations qui permettent de le manipuler.
Proposition 2 : tout peut se représenter sous la forme d'objets conceptuels.
Proposition 3 : les objets sont dans un rapport d'adéquation avec le monde. Ils ne peuvent être affirmés, postulés ou réfutés.
Les concepts fondamentaux
Réification
Définition : la réification est l'opération par laquelle quelque chose (chose physique, relation, événement, situation, idée, lois, etc....) est représentée de façon informatique sous la forme d'un objet.
Notation
Cette opération de réification est au cur de l'approche objet. C'est par ce processus que l'on peut répondre à la question : quels sont les objets que je manipule et comment doit-on les représenter ? Nous reviendrons longuement sur ce processus quand nous aborderons les méthodes de conception objet dans la sixième partie.
En fait, il est difficile d'associer un unique concept à une chose. Le plus souvent, le processus de réification dépend de la personne concernée, de son point de vue sur l'objet, c'est-à-dire de façon plus générale du contexte dans lequel s'opère cette réification.
On peut alors trouver deux types d'approches.
· Une approche subjective qui associe une représentation du monde à un contexte. Chaque personne, dans chaque contexte particulier construit sa représentation de la chose.
· Une approche objective qui associe plusieurs représentations ou points de vue au même objet. Ces points de vue sont attachés à la chose, et décrivent autant d'aspects objectifs de l'univers, censé être indépendant du sujet.
Nous verrons que c'est cette approche qui est en général utilisée en ingénierie.
Dénotation
Définition : la dénotation est l'opération qui associe un concept à une chose réelle. Le concept (l'objet informatique) représente la chose. C'est l'opération inverse à la réification.
Trois aspects des objets
Selon Ferber [Ferber & Ghallab] on peut considérer les objets sous trois points de vue complémentaires :
Aspect structurel : un objet est une structure de donnée définie par un type et ses opérations.
Aspect conceptuel : un objet représente quelque chose du monde abstrait ou concret.
· Point de vue représentation des connaissances
· Intelligence artificielle, base de données objet
Aspect actanciel : un objet est un agent autonome capable d'interagir avec d'autres agents par envoi de messages.
Les langages objets
Nous allons tous d'abord rappeler les caractéristiques essentielles communes à la majorité des langages objets et que nous appellerons ici modèle objet de base. Ce modèle est en cours de définition par l'OMG (Object Management Group), une organisation qui vise à promouvoir l'utilisation de l'approche objet et des langages objets.
Modèle objet de base
Un objet peut servir à modéliser n'importe quel type d'entité : par exemple une personne, un document, une pièce, une matière, un fichier, une fenêtre, ou un analyseur syntaxique.
Définitions
Objet
Un objet est une entité ayant une identité propre, possédant un ensemble d'opérations et un état qui mémorise les effets de ces opérations.
En général un objet est constitué de trois types de composants élémentaires.
Ses attributs : son état propre
Ses relations : ses liens avec d'autres objets
Ses méthodes : ce qu'il sait faire
Pour des raisons pragmatiques, dans de nombreux langages, on fait souvent une distinction entre les objets et des non-objets (ou types simples) qui caractérisent les éléments de base du langage (booléen, nombre entier, réel, caractère, chaîne de caractères, date, etc...). Un non-objet n'a pas d'identité propre, et ne peut pas exécuter une opération.
La distinction attribut/relation provient alors du fait que l'on veut faire la différence entre un lien avec un non-objet et un lien avec un objet "réel" (personne, pièce, etc...).
Attributs
Les attributs peuvent être typés, on peut éventuellement leur attacher des démons. Certains attributs doivent pouvoir être déclarés comme étant indexés, afin de créer des points d'entrée dans la base.
Relations
Les relations peuvent être binaires ou n-aires, et pouvoir éventuellement porter elles mêmes des attributs.
Méthodes
Les méthodes définissent le comportement des objets, elles sont généralement mises en facteur au niveau d'une classe. Il est intéressant de pouvoir considérer les méthodes comme des objets à part entière, afin de pouvoir les stocker en tant que telles.
Type
Les objets ayant les mêmes comportements (les même opérations) sont groupés par types. Un type caractérise le comportement de ces instances en décrivant les opérations pouvant être appliquées à celles-ci. Les types peuvent être organisés en une hiérarchie par une relation d'héritage.
Héritage
L'héritage peut être simple (arbre) ou multiple (réseau acyclique). Lorsque l'héritage est multiple, il faut définir précisément le sens de parcourt du graphe. Pour plus de détails, lire [Ducourneau & Habib 89]. L'héritage peut s'appliquer de façon différente sur les attributs, les relations et les méthodes, avec notamment diverses possibilités de surcharge.
Typologie des langages objets
On ne peut pas définir simplement ce que sont les langages objets car ceux-ci présentent une large gamme de caractéristiques différentes.
Stefik et Bobrow définissent les objets comme des "entités qui combinent les propriétés des procédures et celles des données car ils effectuent des calculs et sauvegardent un état local" [Stefik & Bobrow.86].
Pour Booch, le modèle objet est essentiellement défini par les quatre caractéristiques suivantes :
Auquel il joint trois autres caractéristiques qui bien qu'utiles ne sont pas indispensables au modèle objet :
On peut trouver dans [Wegner 87] une tentative de classification en identifiant 6 propriétés (appelées dimensions par Wegner) qui permettent de caractériser ces langages. Ces propriétés ont comme caractéristique d'être consistantes et orthogonales. Elles sont consistantes car il est possible de les retrouver réunies dans un même langage. Elles sont orthogonales, c'est-à-dire indépendantes, car pour chaque sous ensemble de ces caractéristiques, il est possible de trouver un langage qui possède ce sous ensemble de propriétés, et aucune du sous ensemble complémentaire. Du point de vue méthodologique, l'orthogonalité est un concept important, car il permet une meilleure classification.
Les propriétés identifiées par Wegner sont :
Objets
Un objet est une entité possédant un ensemble "d'opérations" et un "état" qui mémorise les effets de ses opérations. Les objets sont à opposer aux fonctions, qui elles n'ont aucune "mémoire"
Types
Un type est une spécification de comportement qui peut être utilisé pour générer des instances ayant ce comportement. La notion de type est le plus souvent équivalente à la notion de classe dans les langages objets. Le typage peut être statique ou dynamique, et peut être plus ou moins fort
Délégation
La délégation est un mécanisme par lequel un objet donne procuration à un autre objet "ancêtre" pour obtenir une valeur ou exécuter une opération. La délégation est essentiellement un mécanisme de partage qui permet à un objet de considérer que les ressources de ses ancêtres sont aussi les siennes. On distingue couramment deux grands mécanismes de délégation : l'héritage et la délégation.
Héritage : le mécanisme d'héritage est le plus connu dans le domaine des langages objets. Il est intimement lié à la notion de classe.
Délégation : c'est le mécanisme qui est utilisé dans les langages à base de prototypes.
Abstraction
Par abstraction de données, on désigne le fait que l'état d'un objet n'est accessible que par l'intermédiaire de ces opérations. C'est aussi ce que l'on appelle l'encapsulation des données.
Concurrence
La concurrence est la capacité pour des objets d'exécuter simultanément dans le temps diverses opérations. La concurrence suppose l'existence d'un certain nombre de mécanismes d'accès et de partage de ressources.
Persistance
La persistance est la capacité pour un objet de perdurer plus longtemps que le programme qui lui a donné naissance. La persistance suppose en général un mécanisme de stockage sur un support permanent.
On peut alors donner les définitions suivantes :
Langage orienté objet = objets + classes + héritage
Langage prototypique = objets + délégation (pas de classes)
Langage acteur = objets + abstraction + concurrence
Représentation et ingénierie
Une information peut avoir un grand nombre de caractéristiques, et ces caractéristiques influent sur l'utilisation que l'on peut en faire.
· Une donnée peut avoir un historique : on peut savoir a quel moment elle à été établie, et par qui. Elle peut éventuellement avoir été modifiée ensuite, et l'on a pu alors noter la date et les raisons ce changement.
· Elle peut résulter d'hypothèses ou de croyances, et donc il est important de la rattacher au contexte particulier qui lui a donné naissance pour qu'elle puisse garder tout son sens.
· Une information peut être plus ou moins importante dans un contexte donné. Il est donc souhaitable de représenter et de stocker les données les plus pertinentes de façon particulière pour pouvoir les retrouver et les manipuler le plus efficacement possible.
Toutes les informations ou connaissances sur de l'information est ce que l'on appelle des méta-informations ou des méta-connaissances. Le domaine des méta-connaissances est notamment très bien abordé dans [Pitrat 90].
Nous allons dans cette partie plus particulièrement nous intéresser aux méta-informations, c'est-à-dire aux données sur les données.
Nous allons tout d'abord essayer de faire un inventaire des différentes méta-informations et donc par la même aborder le premier problème de la représentation des connaissances : qu'est-ce qui doit être modélisé ?
Puis nous aborderons les différentes approches existantes pour représenter ces méta-informations et ainsi traiter le second problème de la représentation des connaissances : comment modéliser ?
Les méta-informations
Unité
Les types de données utilisés dans les langages de programmation permettent de définir des ensembles de valeurs et les opérations à appliquer sur ces valeurs, mais il ne permettent en général pas de spécifier d'autres types de propriétés associés aux objets du monde réel tel que les unités de mesure [Cmelik & Gehani 88]. Le fait d'associer explicitement une unité aux valeurs peut permettre :
- de détecter les erreurs provenant d'opérations entre valeurs aux unités incompatibles.
- d'effectuer des conversions automatiques entre unités équivalentes.
- de mieux documenter les programmes en définissant mieux les variables.
- de faire de l'analyse dimensionnelle.
Dans un langage classique tel que C ou LISP, le compilateur (ou l'interpréteur) ne dispose que d'informations sur le type des variables utilisées. S'il disposait en plus d'informations sur les unités associées à ces variables il serait alors capable de détecter des erreurs provenant d'opérations entre valeurs aux unités incohérentes.
longueur + aire : illégal, car unités de dimensions différentes
aire = volume : illégal car la variable et la valeur sont incompatibles
De plus, connaissant les unités associées aux variables, et ayant par ailleurs défini les règles de conversion entre unités de même dimensions, il est possible d'effectuer des conversions automatiques entre unités. Par exemple : A(m) = B(cm) + C(mm)
Enfin, l'utilisation d'unités associée aux variables dans un programme, peut permettre de mieux documenter celui-ci, et de rendre explicite ce qui ne l'est pas toujours.
Pour l'utilisateur, il est important de pouvoir choisir l'unité par défaut dans lequel seront représentées toutes les dimensions. Lorsque l'on aura besoin de renseigner des valeurs, on donnera à la fois une valeur numérique, et une unité si l'on désire utiliser une unité autre que celle par défaut. En fonction de l'unité, la valeur entrée sera convertie automatiquement.
Etat et validité
Dans un processus industriel, il est très important de connaître l'état d'une donnée. Une donnée peut en effet exister sous plusieurs états, depuis un état "brouillon" jusqu'à un état "figé" ou "contractuel". Une donnée peut en effet être plus ou moins valide, et plus ou moins stable. Il y a en effet une différence très importante entre une donnée sur une pièce en phase d'avant projet, en phase de conception détaillée, en phase de fabrication, et cette même donnée une fois la pièce livrée au client. Alors que la première peut être le résultat d'un certain nombre d'hypothèses, et peut être facilement remise en cause, la dernière est totalement figée, et peut être soumise à des clauses contractuelles. De plus entre chaque étape, cette donnée a été soumise à un certain nombre de contrôles, donnant lieu a des actions de validation.
A une donnée sera en général associé un propriétaire (ou créateur), c'est-à-dire la personne qui lui a donné naissance, et un ou plusieurs responsables qui auront eû pour rôle de vérifier sa validité. De même suivant son statut ou état, on associera à une donnée un niveau de visibilité ou d'accès pour les autres utilisateurs. Une donnée sur laquelle travaille une personne n'a de sens que pour celle-ci, alors qu'a l'autre bout du spectre, une donnée sur un produit livré doit pouvoir être consulté par n'importe qui (mais ne doit plus pouvoir être modifiée).
Il sera donc important de pouvoir représenter les notions de validation (correspondant à un contrôle de type technique), d'approbation (correspondant à un contrôle de type contractuel), ainsi que les droits d'accès aux données.
De façon générale pour avoir une représentation suffisamment riche il sera nécessaire de prendre en compte un certain nombre d'informations associées à la valeur d'un objet ou d'un attribut. On peut notamment citer les propriétés suivantes :
Relations inter-objets
On trouve la notion de relation dans les bases de données relationnelle, et les modèles de donnée sémantiques. La notion de relation y est alors une construction sémantique de base [Rumbaugh 87]. Une relation associe des objets de n classes. L'état d'une relation est un ensemble d'éléments, chaque élément consistant en un objet de chacune des n classes.
On ne retrouve par contre pas cette notion dans les principaux langages objets (Smalltalk, Eiffel, C++, CLOS, etc...). Dans ces langages, il est possible d'utiliser des relations, mais l'utilisation de celles-ci se fera au travers de méthodes spécifiques.
Les langages objets ne contiennent en général pas de syntaxe ou de sémantique permettant d'exprimer la notion générale de relation. Seule deux relations y sont exprimées de façon implicite:
- la relation de classe à sous-classe IS-A
- la relation d'instance à classe INSTANCE-OF
Une modélisation d'un problème fait naturellement appel à la notion de relation, aussi est-il très utile de retrouver dans le langage utilisé cette notion de relation. Il est donc important de ne pas seulement considérer les relations comme de simples facilité d'implantation, mais vraiment comme des constructions sémantiques faisant pleinement partie du langage.
On en arrive alors à un modèle de type OBJET-RELATION, qui combine les concepts d'objet, de classes et de méthodes du modèle objet tels que l'on peut les trouver dans SmallTalk [Goldberg & Robson 83], avec les concepts de relations provenant du modèle ENTITE-ASSOCIATION [Chen 76].
Il est souhaitable de pouvoir déclarer les relations de la même façon que l'on déclare les classes. On déclare une classe en spécifiant son nom, les classes dont elle hérite, et la liste de ses attributs
De même, on définira une relation par son nom, son degré, ses contraintes de cardinalité, et pour chaque champ, le type de classe attendu. Chaque champ pourra éventuellement être nommé afin de permettre une indexation par mot clef.
On pourra également définir une hiérarchie de relations : partant de la classe la plus générale RELATION, et en la spécialisant en sous classes : RELATION-BINAIRE, RELATION-TERNAIRE, etc...
Les méthodes appliquées aux relations seront
- Indexation par champ du tuple
- Parcourt de l'ensemble des valeurs
Les méthodes de mise à jours d'une relation doivent vérifier le type de ses arguments et leurs cardinalité. Il existe deux façons de traiter une relation.
--> on envoie un message à la relation
--> on envoie un message à l'une des classes participant à la relation
Les deux formes doivent être équivalentes, et un compilateur doit pouvoir faire automatiquement la traduction d'une forme dans une autre.
Versions
Il est important de pouvoir stocker les versions successives d'un objet et l'évolution des relations de cet objet avec d'autres objets [Kim & Chou 86], [Lehman & Katz 84], [Zdonik 86a]. Le terme de version inclue en fait plusieurs notions :
- Historique des modifications apportées à un objet
- Alternatives dans la conception d'un objet
- Gestion de différentes configurations d'un objet
- Génération d'hypothèses sur un objet
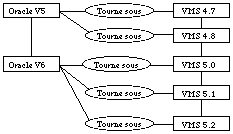
On peut par exemple vouloir représenter le problème classique de gestion de configuration informatique : telle version d'un produit nécessite telle révision du système d'exploitation
Versions internes et externes
On peut classer les versions en deux catégories.
· Les versions externes ou versions applicatives qui consistent en différentes versions (ou plutôt configurations) d'un produit du point de vue de l'utilisateur.
· Les versions internes ou versions systèmes qui sont des versions des objets générées et gérées par le système lui même.
On fait souvent l'amalgame entre ces deux types de versions alors que pour l'utilisateur, seules les versions externes importent.
Cohérence des versions
Le principal problème à résoudre pour gérer correctement les versions d'un objet est de maintenir la cohérence des liens entre les différents objets quand ces objets peuvent exister sous plusieurs versions différentes. Le problème devient crucial lorsque l'on doit gérer des configurations composées d'un nombre d'objets très important, chacun pouvant avoir plusieurs variantes.
Graphe des versions
Pour connaître la façon dont les différentes versions sont reliées entre elles, il est habituel de les organiser en un graphe appelé graphe des versions (version graph). Ce graphe permet de dire quels sont les liens entre les différentes versions, quelle version a donné naissance à telle autre. Ce graphe peut exister pour chaque objet, et dans ce cas il est appelé graphe local de versions [Klahold et al 86], [Zdonick 86a], ou bien il peut être défini de façon globale et unique pour tous les objets en quel cas on parle alors de graphe global de versions [Barthes 91].
Que le graphe de versions soit local ou global, il doit permettre de représenter l'histoire, c'est-à-dire la succession des différentes versions d'un objet.
Ce graphe peut être linéaire, auquel cas les versions représentent simplement l'évolution d'un objet au cours du temps. On retrouve notamment cette notion de versions linéaires dans un système d'exploitation tel que VMS, ou chaque modification d'un fichier provoque automatiquement la création d'une nouvelle version.
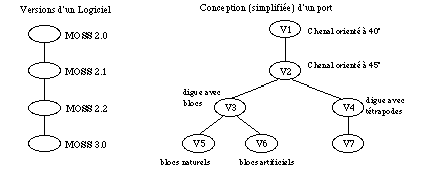
Ce graphe peut aussi être un arbre, ce qui permet alors la création de versions parallèles ou alternatives. La possibilité de pouvoir créer des alternatives est très importante car elle permet notamment en conception d'évaluer en parallèle plusieurs hypothèses en partant d'un même état initial [Monceyron 91], [Thoraval 91]. Cela permet aussi de modéliser le fait courant notamment dans l'industrie du logiciel qu'une équipe peut assurer la maintenance d'un produit, pendant que simultanément une autre équipe travaille déjà à développer la version suivante.
Graphe linéaire et arbre de versions.
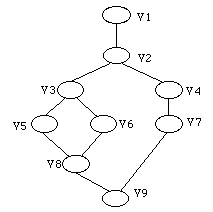
Ce graphe peut finalement, et c'est alors le cas le plus général, être un graphe acyclique orienté, que qui permet non seulement d'avoir des versions alternatives, mais aussi de pouvoir faire la fusion (merging) de ces alternatives ( See Graphe acyclique avec fusion de versions ).
Graphe acyclique avec fusion de versions
En conception, cette notion de fusion correspond à la synthèse de plusieurs hypothèses ou options de design, pour garder le meilleur de chacune. Dans le cas du génie logiciel, cela peut correspondre à la prise en compte par l'équipe de développement, d'un certain nombre de bogues répertoriées et corrigées par l'équipe de maintenance. C'est d'ailleurs dans le domaine du génie logiciel que l'on trouve les meilleurs exemples de gestionnaires de versions avec des programmes tels que SCCS [Sun 88a], [Sun 88b], RCS [Tichy 82] et CVS [Berliner].
Nous verrons plus loin dans le chapitre IV que l'on retrouve aussi cette notion de version dans certaines bases de données orientées objets.
Hypothèses
On trouve cette notion proche de celle de version (appelée états dans SMECI [Smeci 90], monde dans KEE, ou de point de vue (viewpoints) dans ART [ART 85]) lorsque l'on fait des raisonnements hypothétiques à l'aide d'un système expert. Il est alors nécessaire de stocker et d'indexer ensemble les objets cohérents avec un ensemble d'hypothèses.
Gestion des hypothèses dans SMECI
SMECI est capable d'effectuer un raisonnement hypothétique en utilisant des contextes parallèles nommés états. Un état est un contexte global défini par l'ensemble des valeurs des champs de tous les objets. La succession de ces contextes forme un arbre d'états, dont la racine est l'état initial du raisonnement, et les feuilles sont soit des solutions, soit des impasses pour le problème traité. Cet arbre d'état sert également d'historique du raisonnement, c'est grâce à lui que l'on pourra bâtir des explications ou établir des comparaisons.
Une particularité de SMECI est que ces valeurs sont stockées sous forme différentielle. On n'enregistre que des transitions : affectation d'une valeur, création ou destruction d'objets. Un état est donc entièrement déterminé par son père, et l'ensemble des transitions par rapport à ce père. Le passage d'un état à un autre se fait par un mécanisme de faire/défaire, en parcourant l'arbre des états. Cette technique, si elle est naturelle en cas de retour arrière (Backtraking), peut néanmoins se révéler assez coûteuse si l'on désire basculer entre deux états très distants dans l'arbre. Une table de hachage auxiliaire permet de détecter les états identiques, et donc d'éviter de boucler dans un raisonnement.
Gestion des hypothèses dans ART
Un fait est crée par assertion dans un "viewpoint". Ce fait sera alors vrai dans ce viewpoint et dans tous les viewpoints qui en héritent. Le fait peut être rétracté de l'un ou de plusieurs des viewpoints qui héritent du viewpoint où il a été asserté. Un extent définit l'ensemble des viewpoints dans lesquels un fait est vrai. En général, un extent est défini par un viewpoint de base où le fait a été asserté, et un ensemble de viewpoints où le fait a été rétracté.
Un extent est représenté par les symboles [) reprenant la notion mathématique d'intervalle demi-ouvert. Un fait asserté dans un viewpoint v, et rétracté dans les viewpoints r1 et r2 sera vrai dans l'extent noté [v | r1 r2)
A l'heure actuelle ces mondes hypothétiques sont créés en mémoire par les différents générateurs de systèmes experts cités, mais il n'existe aucun moyen de les sauvegarder de façon permanente (sauf en générant une image mémoire).
Représentation du temps
Le travail de [Snodgrass 86] sur les bases de données temporelles a montré que le temps peut être modélisé et représenté suivant deux dimensions dont les axes sont le temps de transaction et le temps réel [Nestor 86].
· En se déplaçant le long de l'axe de temps de transaction, on peut se placer dans un état logique du système au moment d'une transaction donnée.
· En se déplaçant le long de l'axe du temps réel, l'on obtient une représentation de la réalité à cette époque (telle qu'on a pu la percevoir).
Le temps de transaction et le temps réel diffèrent soit par ce qu'il y a eu un délai entre l'événement concret, et le moment où on l'a entré dans la base, ou parce qu'un événement a été saisi de façon erronée, et qu'on a apporté des corrections ultérieurement.
Un troisième axe pourrait représenter l'évolution des fonctionnalités d'un produit (logiciel, définition d'une pièce, etc...).
Une quatrième dimension serait la création d'hypothèses, et donc autant de branches parallèles du temps.
Représentation de l'espace
Des domaines tels que la conception architecturale et la conception en ingénierie, doivent souvent prendre en compte la représentation et le placement d'objets dans un espace à deux ou trois dimensions. Il est donc important de disposer d'une représentation de l'espace et des objets dans cet espace.
On peut par exemple trouver dans [Maculet 91] un exemple de représentation permettant de résoudre des contraintes de placement spatial en architecture. Il consiste à utiliser une représentation discrète de l'espace utilisant des boîtes englobant les objets et appelées boites de Manhattan.
Les différents modèles de représentation
Les langages objets permettent en général une représentation des attributs limitée à la seule valeur de cet attribut (cette valeur pouvant parfois être multivaluée). Dans certains langages, on peut parfois factoriser une information globale au niveau de la définition de la propriété, par exemple sa valeur par défaut. Ce type de représentation est très pauvre et ne permet pas d'ajouter des méta-informations sur la valeur de cet attribut. Ce problème est notamment évoqué dans [Ferber 89].
Pour permettre une représentation beaucoup plus riche des informations et des méta-informations, plusieurs mécanismes ont été proposés :
- utiliser un format de facettes, comme le font la plupart des langages de frames,
- utiliser un format utilisant des descripteurs objets d'attributs,
- utiliser une technique de "clonage" pour les liens qui le nécessitent (Barthès),
- déclarer qu'une propriété est représentée par une classe, et que chaque utilisation de cette propriété est réellement une instance de cette classe (Ferber),
- utiliser des objets d'annotation (Lenat).
Nous allons donc passer en revue ces différentes solutions en présentant à chaque fois un ou plusieurs exemples de systèmes utilisant ces différents types de représentations.
Frames
Le format général d'un frame possède normalement trois niveaux: frame / slot / facet. On en trouve un parfait exemple dans le langage RLL.
RLL [Greiner & Lenat 80] est un langage qui a été conçu comme un outil permettant de construire des langages de représentation de connaissances, d'où son nom : RRL = Représentation Language Language. RLL est un langage auto descriptif de type "Frame" où les objets constitués de "slots" sont appelés UNITS. Il est constitué comme une bibliothèque de composants permettant d'implanter un certain nombre de mécanismes de base tels que : héritage, fonction d'accès aux slots (Put, Get), attachement procédural, mécanismes de contrôle (backtrack, agenda), etc...
A partir de ces briques de bases (il existe quelques 106 "slots" initiaux), il est ensuite possible de personnaliser le système pour l'adapter à ses besoins propres. Il est par exemple possible de redéfinir son propre algorithme d'héritage. RLL sait faire la différence entre la sémantique et la syntaxe, c'est-à-dire le fait que certains slots (couleur, age) servent à représenter la connaissance du monde, alors que d'autres (date_de_creation_du_slot, nb_de_slots) servent uniquement à représenter la structure interne du langage.
Descripteurs d'attributs
On trouve par exemple ce type de représentation dans un système tel que SMECI. SMECI (pour Système Multi-Expert de Conception en Ingénierie) est un environnement de développement d'applications à bases de connaissances [Smeci 90]. Il a été initialement développé pour résoudre des problèmes dans des domaines tels que la conception, la simulation, le diagnostic complexe et la planification.
Dans Smeci, chaque objet est instance d'une classe unique appelée catégorie. Une catégorie est décrite par ces champs qui définissent ses propriétés caractéristiques. Les catégories sont organisées en un arbre de spécialisation.
Pour représenter et mettre en facteur certaines informations communes à tous les objets d'une catégorie, on utilise un objet particulier appelé prototype qui est attaché a chaque catégorie. Le prototype permet de préciser et de restreindre le domaine de validité des champs définis dans une catégorie, ainsi que de mettre en commun certaines valeurs communes à toutes les instances de la catégorie.
Ce système permet de d'établir une séparation entre les informations structurelles (les champs portés par les catégories), et des contraintes et connaissances (porté par les prototypes) qui sont issues de la modélisation de l'application. Les champs contiennent différentes facettes définies aux trois niveaux correspondant à la structuration catégorie/prototype/objet.
Au niveau de la catégorie : nom, type, catégorie de la valeur associée, unité, lien inverse, etc...
Au niveau du prototype : domaine de valeur
Au niveau de l'instance : valeur du champ.
Parmi les types de champs, certains peuvent référencer d'autres objets, permettant d'implanter des relations entre ceux-ci. Il est possible de définir des liens inverses entre ces champs, qui seront tenus à jours automatiquement par des démons système en cas d'affectation. Il est enfin possible d'associer une sémantique particulière à ces champs. On dispose notamment du lien prédéfini : subpart, qui permet de représenter une relation de partie à sous-partie entre objets.
Attributs objets
Cette approche, développée par Ferber dans sa thèse [Ferber 89], est sans doute la technique la plus générale. Elle consiste à considérer les attributs comme des objets à part entière.
Objets annotation
L'approche de Lenat consiste à ajouter des objets contenant toutes les méta-informations sous forme d'annotations. La présence d'annotation est indiquée par le macro-caractère .
Lenat et Guha développent l'exemple suivant, illustrant l'utilisation répétée d'annotations sur une propriété puis sur une valeur.
Texas
capital: (Austin)
residents: (Doug Guha Mary)
stateOf: (UnitedStatesOfAmerica)
residents
instanceOf: (Slot)
inverse: (residentOf)
makesSenseFor: (GeopoliticalRegion)
entryIsA: (Person)
specSlots: (lifeLongResidents illegalAliens registeredVoters)
slotConstraint: ((coTemporal u v))
SeeUnitFor-residents.Texas
instanceOf: (SeeUnit)
modifiesUnit: (Texas)
modifiesSlot: (residents)
rateOfChange: ()
cardinality: (10,000,000)
SeeUnitFor-rateOfChange.SeeUnitFor-residents.Texas
instanceOf: (SeeUnit)
modifiesUnit: (SeeUnitFor-residents.Texas)
modifiesSlot: (rateOfChange)
qualitativeValue: (Low)
SeeUnitFor-Guharesidents.Texas
instanceOf: (SlotEntryDetailTypeOfSeeUnit)
modifiesUnit: (Texas)
modifiesSlot: (residents)
modifiesEntry: (Guha)
becameTrueIn: (1987)
moreLikelyThan:: (SeeUnitFor-PickUpTruckownsA.Mary)
Cette approche n'a d'intérêt que si les méta-informations sont l'exception. Les valeurs étant de toute façon annotées pour l'utilisation interne, Cyc utilise un format mélangeant facettes et objet annotation. Un certain nombre de facettes sont enregistrées explicitement au niveau de chaque valeur. Ce sont les facettes correspondant aux méta-informations les plus utilisées. On note donc un souci d'efficacité dans la représentation.
Utilisation de descriptions
On trouve notamment ce type de représentation dans le langage OMEGA [Hewitt et all 80]. Ce langage est un système de représentation de connaissances sous forme de taxonomies conceptuelles. Il combine les mécanismes du calcul des prédicats, des systèmes typés, et des systèmes basés sur le Pattern Matching. OMEGA est décrit par ses auteurs comme étant un calcul des descriptions, il est en effet essentiellement basé sur la notion de description. Par exemple :
Cette description définie l'ensemble des pièces composites. Une telle description peut être rendue plus explicite en spécifiant certains attributs. Par exemple :
(a PieceComposite (With type 1) (with classe_drapage 3))
Il est possible de décrire l'appartenance d'un individu à un ensemble :
(Piece45 is (a PieceComposite))
(Piece45 is (a PieceComposite (with validée_par Pierre)))
L'une des caractéristiques d'OMEGA est d'être une logique complètement axiomatisée, dont la consistance et la complétude ont été prouvées [Attardi & Simi 81]. Il est de plus doté d'un métalangage, et permet la représentation de points de vue multiples permettant de faire de la gestion d'hypothèses [Attardi & Simi 85].
Le modèle PDM (Property Driven Model)
Le modèle PDM (Property Driven Model), développé à l'Université de Technologie de Compiègne [Barthes et al 79], est un modèle de représentation basé sur une approche objet. L'objectif initial était de pouvoir accommoder un grand nombre d'objets changeant dynamiquement et de les stocker de façon permanente dans une base de données (appelée VORAS). PDM comporte une structure de schéma à deux niveaux (plutôt que les trois niveaux classiques : schéma, attributs, facette), dans lequel l'attribut ne contiendrait que la facette valeur. Pour compenser la perte de méta-informations liée aux autres facettes, PDM définit les attributs comme des objets eux-mêmes. Les autres facettes deviennent alors des attributs de l'objet attribut.
Ce modèle considère que l'on peut représenter le monde réel comme étant constitué d'objets ou entités, ces entités elles même possédant un certain nombre attributs ou propriétés.
Dans ce modèle, les propriétés ont une existence propre et précèdent les entités (d'où le nom de modèle dirigé par les propriétés). On peut en effet parler d'une propriété NOM ou d'une propriété COULEUR de façon abstraite et générale. Une fois définis, on peut alors créer différents objets. Ces objets auront alors une réelle existence dès qu'ils se seront vus attribués et renseignés certaines de ces propriétés.
Les objets sont représentés par des paires attribut-valeurs. On distingue deux types d'attributs objets : certains ont des valeurs associées et sont appelés propriétés terminales, d'autres implantent des liens entre objets et sont appelés propriétés de structure. Les propriétés et les modèles (les classes) sont à leurs tour représentés comme des objets. De plus, certaines propriétés peuvent être partagés entre les objets.
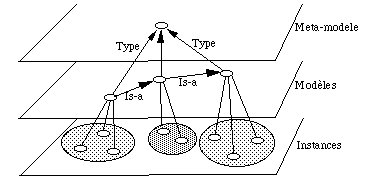
Le modèle PDM est extrêmement souple et s'accommode très facilement de modifications dynamiques. De plus, son aspect méta-circulaire, ou auto-descriptif, permet de manipuler modèles et structure d'objets. Il existe trois niveaux d'objets ( See Niveaux du modèle ensembliste PDM )
- les modèles, formant une hiérarchie IS-A (treillis),
Niveaux du modèle ensembliste PDM
Les instances ont une propriété terminale TYPE spécifiant le nom du modèle, les modèles sont de type ENTITE (méta-modèle), et sont liés dans une hiérarchie IS-A.
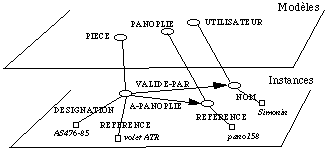
Les objets
Par exemple on créera les objets suivants ( See Un exemple d'instances PDM. ), représentant le fait que la pièce de référence AS456-65 dont la désignation est "volet arrière ATR" a été validée par l'utilisateur dont le nom est "Simonin", et est associée à la panoplie dont la référence est pano158
Les classes
Dans PDM, chaque objet et attribut est lui même instance d'un modèle.
terminal-property-of UTILISATEUR
has-method =if-added, =print-value, =entry
terminal-property-of PIECE, PANOPLIE
has-method =if-added, =print-value, =entry
Ici has-property-name est elle même une propriété terminale, has-method et is-terminal-property-of sont des propriétés de structures liant NOM au modèle d'utilisateur, et à des instances de méthodes (=if-added, =print-value, =entry).
La propriété de structure VALIDE-PAR est décrite de manière identique.
is-structural-property-of PIECE
De même, voici les définitions des classes PIECE, UTILISATEUR, PANOPLIE.
has-terminal-property REFERENCE, DESIGNATION
has-structural-property VALIDE-PAR, A-PANOPLIE
has-method =summary, =print-self,...
has-method =summary, =print-self,...
has-terminal-property REFERENCE
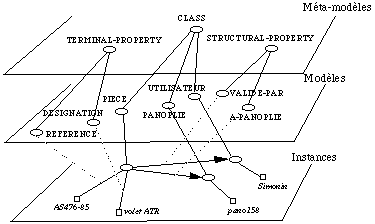
Le méta-modèle
Le méta-modèle est constitué des trois classes CLASS, TERMINAL-PROPERTY et STRUCTURAL-PROPERTY ( See Le méta-modèle PDM. ).
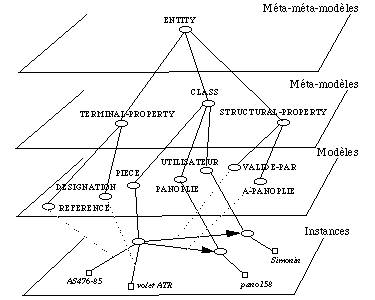
Méta-méta-modèle
Finalement on introduit une classe nommé ENTITY spécifiant la structure du méta-modèle. ENTITY est alors son propre modèle (modèle auto réflexif) ( See Le Méta-méta-modèle PDM. ).